直接插入排序算法
- 概述
直接插入排序算法在逻辑上将整体数据分为两部分,一部分是已排序部分,另一部分是待排序部分 。
排序的过程是:在待排序部分逐步的拿出一个元素,将其插入到已排序部分中合理的位置 。 - 适用场景
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率,
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位 。 - 优化
在给当前待排序元素在已排序部分找到一个合适的位置并且待排序数据相对较多的时候,由于已排序部分元素是有序的,因此这个过程可以使用二分法,以优化排序的时间复杂度。 - 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 稳定排序算法。
- 空间复杂度
直接插入排序是in-place,因此其空间复杂度是 O(1) 。 - 时间复杂度
- 最优
最优的情况是待排序数据为已排序好的期望顺序,此时每次从待排序部分拿出一个元素只需要与待排序部分中最后一个元素相比较一次,需要比较 $n - 1$ 次,因此其复杂度为 $O(n)$ 。 - 最坏
最坏的情况是待排序数据为已排序好的,但是其顺序正好与期望顺序相反,此时每次从待排序部分拿出一个元素,该元素需要与其前面的已排序部分中的每一个元素进行比较和交换,其比较或交换的次数为 $0+1+2+…+(n-2)+(n-1)$ 也就是$\frac{n*(n-1)}{2}$ , 因此其复杂度为 $O(n^{2})$(是n方,恶心的渲染器) 。 - 平均
$O(n^{2})$
- 最优
- 代码示例
1
2
3
4
5
6
7
8
9
10
11
12void insertion_sort(int arr[], int len){
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
希尔排序算法
- 概述
希尔排序是插入排序的一个优化版本,是在插入排序的基础上加入了分治的思想,按照设置好的步长进行跳跃式的插入排序,或者说按照步长将数据分为几个部分,分别对这几个部分进行排序。举个例子:有一组数据arr有10个元素,我们设步长为5,排序的开始,定位到首位元素,首位元素是他们组的第一个元素,它们组的第二位元素应该是$arr[0+5]$ 也就是第5个元素。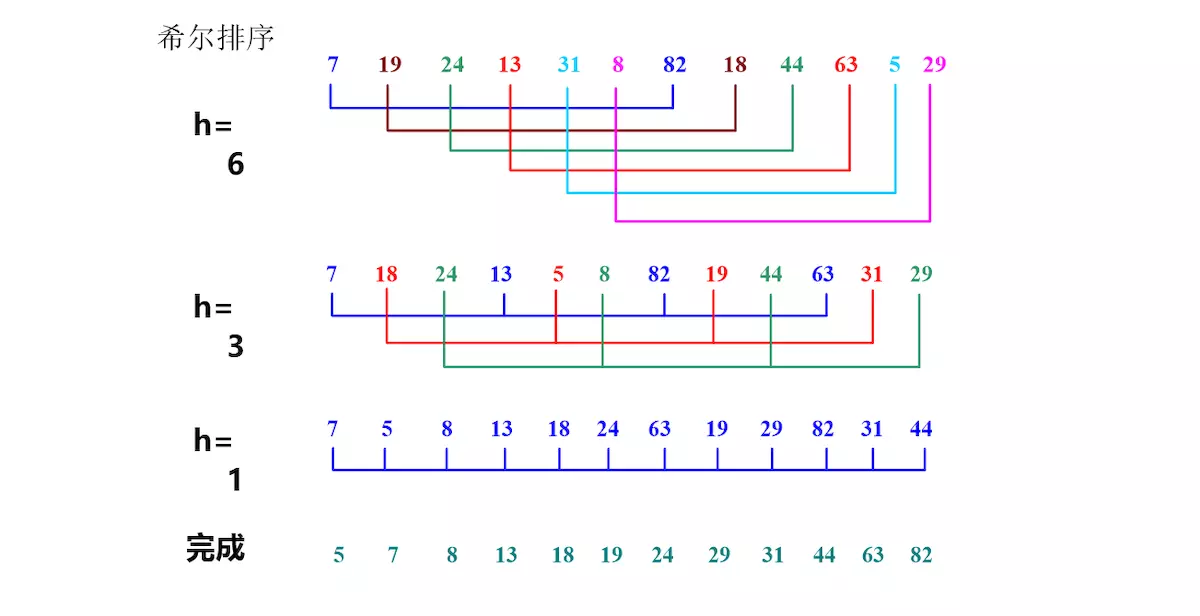
- 适用场景
在shell先生的优化下,希尔排序不仅继承了插入排序的优点,而且可以做到对于数据量稍微大点的,无序的数据也能很快。 - 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 不稳定排序算法。
- 空间复杂度
与插入排序相同,它是一个原地算法,它的时间复杂度是线性的,也就是$O(1)$ 。 - 时间复杂度
希尔排序的时间复杂度与步长的选取有关,当步长为1的时候,时间复杂度是$O(n^{2})$ 。
当采用Sedgewick提出的步长(目前最好的步长序列)的时候,时间复杂度为$O({n}log_{2}{n})$ 。 - 代码示例
1
2
3
4
5
6
7
8
9
10
11void shell_sort(int arr[], int len) {
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
for (i = gap; i < len; i++) {
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}
简单选择排序算法
- 概述
选择排序依然是将待排序数据分为已排序区和待排序区。
排序的逻辑是每次从待排序区找出一个最大(或最小)的元素放置到已排序区的末尾。
选择排序算法是所有纯基于交换的排序算法中非常好的。 - 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 不稳定排序算法。
- 空间复杂度
它是一个原地算法,它的时间复杂度是线性的,也就是$O(1)$ 。 - 时间复杂度
其最好、最坏和平均的时间复杂度都是$O(n^{2})$ 。 - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20void selection_sort(int a[], int len)
{
int i,j,temp;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++) //走訪未排序的元素
{
if (a[j] < a[min]) //找到目前最小值
{
min = j; //记录最小值
}
}
temp=a[min];
a[min]=a[i];
a[i]=temp;
}
}
堆排序
- 概述
堆排序也属于选择排序。
利用堆的特性对数据进行排序的一种排序算法。
排序的逻辑就是不断的从堆顶弹出一个元素,然后每次弹出一个元素后维护一下堆,当堆空的时候排序完成。 - 适用场景
- 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 不稳定排序算法。
- 空间复杂度
堆排序属于原地算法,空间复杂度为$O(1)$ - 时间复杂度
平均时间复杂度为$O(nlogn)$ - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
void swap(int *a, int *b) {
int temp = *b;
*b = *a;
*a = temp;
}
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { // 若子節點指標在範圍內才做比較
if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢,直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比较
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
int i;
// 初始化,i從最後一個父節點開始調整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已排好元素前一位做交換,再重新調整,直到排序完畢
for (i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
冒泡排序
- 概述
冒泡排序是非常经典的一个纯粹基于交换的排序算法。
算法的基本逻辑是:对于n个待排序数据,有n次循环,每次循环从第一个元素开始与其后面的元素相比较,对相对位置不对的两个元素实施交换,循环结束后本次循环的末尾位置就是本次循环最大的元素,因此每次循环的长度都比上次循环次数少一。 - 适用场景
基本有序,数量较少。 - 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 稳定排序算法。
- 时间复杂度
平均时间复杂度为$O(n^{2})$ - 空间复杂度
原地算法,其空间复杂度为$O(1)$ - 比较次数
循环次数是n次,每次循环都能有一个当前最大的元素归位,因此每次循环的长度都比上次循环次数少一,那么对于n个待排序数据,其比较次数就是$(n-1) + (n - 2) + … + 1$ - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/* 泡沫排序 */
/* 1. 從當前元素起,向後依次比較每一對相鄰元素,若逆序則互換 */
/* 2. 對所有元素均重複以上步驟,直至最後一個元素 */
/* elemType arr[]: 排序目標數組; int len: 元素個數 */
void bubbleSort (int arr[], int len)
{
int i, j,temp;
Boolean exchanged = true;
for (i=0; exchanged && i<len-1; i++) /* 外迴圈為排序趟數,len個數進行len-1趟,只有交換過,exchanged值為true才有執行迴圈的必要,否則exchanged值為false不執行迴圈 */
for (j=0; j<len-1-i; j++)
{ /* 內迴圈為每趟比較的次數,第i趟比較len-i次 */
exchanged = false;
if (arr[j] > arr[j+1])
{ /* 相鄰元素比較,若逆序則互換(升序為左大於右,逆序反之) */
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
exchanged = true; /*只有數值互換過, exchanged才會從false變成true,否則數列已經排序完成,exchanged值仍然為false,沒必要排序 */
}
}
}
int main (void) {
int arr[ARR_LEN] = {3,5,1,-7,4,9,-6,8,10,4};
int len = 10;
int i;
bubbleSort (arr, len);
for (i=0; i<len; i++)
printf ("%d\t", arr[i]);
putchar ('\n');
return 0;
}
快速排序
- 概述
快速排序也是非常经典而且很实用的一种排序算法,该算法采用了分治的思想。
算法的基本逻辑是每次从当前排序区域挑选出一个基准值,通过不断的交换使得基准值左边的数据都比基准值小(或大),右边相反,
然后以基准值为分割,递归的对两个部分分别进行上述交换。 - 适用场景
数据量较大且混乱程度较高。 - 归类
- in-place(原地算法:基本上不需要额外的空间)。
- 不稳定排序算法。
- 时间复杂度
平均时间复杂度为$O(nlogn)$ - 空间复杂度
原地算法,其空间复杂度为$O(1)$ - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43typedef struct _Range {
int start, end;
} Range;
Range new_Range(int s, int e) {
Range r;
r.start = s;
r.end = e;
return r;
}
void swap(int *x, int *y) {
int t = *x;
*x = *y;
*y = t;
}
void quick_sort(int arr[], const int len) {
if (len <= 0)
return; // 避免len等於負值時引發段錯誤(Segment Fault)
// r[]模擬列表,p為數量,r[p++]為push,r[--p]為pop且取得元素
Range r[len];
int p = 0;
r[p++] = new_Range(0, len - 1);
while (p) {
Range range = r[--p];
if (range.start >= range.end)
continue;
int mid = arr[(range.start + range.end) / 2]; // 選取中間點為基準點
int left = range.start, right = range.end;
do {
while (arr[left] < mid) ++left; // 檢測基準點左側是否符合要求
while (arr[right] > mid) --right; //檢測基準點右側是否符合要求
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--; // 移動指針以繼續
}
} while (left <= right);
if (range.start < right) r[p++] = new_Range(range.start, right);
if (range.end > left) r[p++] = new_Range(left, range.end);
}
}
归并排序
- 概述
归并排序是分治思想的经典应用。
归并排序分为两种操作:
1. 分割:当前待排序数据分割为两部分。
2. 合并:在保持排序顺序的情况下将两部分合并。
递归方式:
1. 不断的对待排序数据进行递归式的平均分割,直到当前数据不多于2个为止。
2. 对当前待排序数据进行均等分割,不断的分别从两个部分中拿出两个元素进行比较,然后按照排序顺序放置到临时区域,如此对两部分进行合并。
迭代方式:
1. 对于待排序数据两两进行按照排序顺序交换。
2. 对于上述得出的若干两个元素组成的数对再次进行与递归方式相同的归并操作。
3. 如此反复,直到只剩一个部分为止。 - 适用场景
与快速排序相同,适用于数据量较大并且较为混乱的情况。 - 归类
稳定排序算法。 - 时间复杂度
平均时间复杂度为$O(nlogn)$ - 空间复杂度
由于进行归并操作的时候需要借助额外的临时空间存储归并后的数据,而这些数据也正是原数据,因此空间复杂度是$O(n)$。 - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58// 迭代方式
int min(int x, int y) {
return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
int *a = arr;
int *b = (int *) malloc(len * sizeof(int));
int seg, start;
for (seg = 1; seg < len; seg += seg) {
for (start = 0; start < len; start += seg * 2) {
int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
int *temp = a;
a = b;
b = temp;
}
if (a != arr) {
int i;
for (i = 0; i < len; i++)
b[i] = a[i];
b = a;
}
free(b);
}
// 归并方法
void merge_sort_recursive(int arr[], int reg[], int start, int end) {
if (start >= end)
return;
int len = end - start, mid = (len >> 1) + start;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
int k = start;
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
while (start1 <= end1)
reg[k++] = arr[start1++];
while (start2 <= end2)
reg[k++] = arr[start2++];
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
int reg[len];
merge_sort_recursive(arr, reg, 0, len - 1);
}
基数排序
- 概述
基数排序是比较特殊的一种排序方法,是唯一的一个不是基于交换的排序算法。
其基本思想是按照待排序数据的每一位进行排序,进行若干次排序。
基数排序有两种排序方式,一种是从低位到高位排序(LSD), 另一种是从高位到低位排序(MSD)。
这里提到的每一位,可以是任意进制的每一位,而位数的选择也直接影响其时间复杂度与空间复杂度。 - 归类
稳定排序算法 - 时间复杂度
基数排序的时间复杂度受到位数的影响,也就是说有多少位当然也就需要排序多少次,因此其时间复杂度为$O(n * k)$,其中k是位数。 - 空间复杂度
每一位的数字的种类就是以什么样的方式来选择位数,分割每一位,若以十进制来分割每一位,那么每一位的数字的种类就有十种。
在对每一位进行排序的时候,就需要类似桶排序的方式进行。
因此,其空间复杂度就是这若干个“桶”,也就是位数,再加上存储待排序数据的数据结构$O(n * k)$,k为位数。 - 代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int maxData = data[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
/* int d = 1; //保存最大的位数
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;*/
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);
int *tmp = new int[n];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
资源引用声明:









